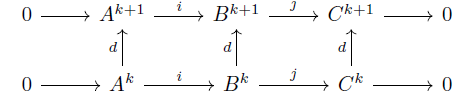Cohomology: Mayers-Vietoris sequence.

Let $U,V$ be an open cover of Manifold $M$. Remember it is very much possible that $U \cap V \neq \emptyset$.
Define the following inclusion maps
\begin{eqnarray}
  i_u:U \rightarrow M, i_u(p) = p \\
  i_v:V \rightarrow M, i_v(p) = p \\
  j_U:U \cup V \rightarrow U, j_u(p) = p \\
  j_V:U \cup V \rightarrow V,j_v(p) = p
\end{eqnarray}
These inclusion map $i_U(p)=p$ from $U$ to $M$ and similar map $i_v(q)=q$ from $V$ to $M$ etc.,

Based on these inclusion maps one can define pull back maps of differentials
\begin{equation}
  i^{*}_U:\Omega^{k}(M) \rightarrow \Omega^{k}(U)
\end{equation}
Similarly one can define a pull back for $i_V$
\begin{equation}
   i^{*}_V:\Omega^{k}(M) \rightarrow \Omega^{k}(V)
 \end{equation}
 Similar pull back maps are defined for $j_U,j_v$.
 \begin{eqnarray}
   j^*_U:\Omega^k(U \cup V) \rightarrow \Omega^k(U) \\
   j^*_V:\Omega^k(U \cup V) \rightarrow \Omega^k(V)
 \end{eqnarray}

 

 By restricting to $U$ and to $V$, we get a homorphism of vector spaces
 \begin{equation}
   i:\Omega^{k}(M) \rightarrow \Omega^k(U) \oplus \Omega^k(V)
 \end{equation}

 defined via
 \begin{equation}
   \sigma \rightarrow (i^{*}_U\sigma,i^{*}_V\sigma)
 \end{equation}

 Using this, define the difference map,
 \begin{equation}
   j:\Omega^k(U) \oplus \Omega^k(V) \rightarrow \Omega^k(U \cap V)
 \end{equation}
 by $j(\omega,\tau)=\tau-\omega$.

 This map indicates what to do with common vectors that belong to both $U$ and $V$. Similar maps are used in Finite dimensional vector spaces to prove dimensionality theorem when $U,V$ are subspaces whose intersection is non-empty.

 Here $\tau,\omega$ are pull backs maps shown before.
 \begin{eqnarray}
   \omega = j^*_U\omega \\
   \tau   = j^*_v \tau
 \end{eqnarray}

 $j$ is a zero map when $U \cup V = \emptyset$.

 Proposition
 For each integer $k \geq 0$, the sequence
 \begin{equation}
   0 \rightarrow \Omega^k(M) \xrightarrow{i} \Omega^k(U) \oplus \Omega^k(V) \xrightarrow{j} \Omega(U \cap V) \rightarrow 0
 \end{equation}
 is exact.

 Proof:
 To show that this exact sequence, we need to show at each node image of previous function to this node is same as kernel from this node to next node.
 We will start with first node - $\Omega^k(M)$.
 $0$ vector maps every function to $0$ in the $\Omega^k(M)$ which is in kernel of $i$. Hence, $im\;(0\rightarrow \Omega^k(M))=ker\;i$.
 
 To prove exactness at $\Omega^k(U \cup V)$, we need to show that $j$ is surjective or onto as next maps takes everything to zero. Thus kernel of next map is all of $\Omega^k(U \cap V)$ which is range of $j$.
 
 We are already given $j$ map in the previous section. This map, together with a very nice partitions of unity, helps us to establish the onto of $j$ map.

 say $\omega \in \Omega^k(U \cap V)$. Let $p_U,p_v$ be functions that form partitions of unity. Define
\begin{eqnarray}
   p_U\omega = \begin{cases}
                 p_v \omega \text{ when }, & x \in U \cap V \\
                 0 \text{ otherwise },& x \in U - (U \cap V)
               \end{cases} \\
  p_V\omega = \begin{cases}
                 p_U \omega \text{ when }, & x \in U \cap U \\
                 0 \text{ otherwise },& x \in V - (U \cap V)
               \end{cases}
 
 \end{eqnarray}
The niceness of partition of unity allows the following to happen.
\begin{equation}
  j(-p_u\omega,p_v\omega)=p_v\omega+p_u\omega=\omega \text{ on } U \cap V
\end{equation}
This shows that $j$ is onto and from the fact the next function sends everything to $0$, we have proved that this is a short exact sequence.

Cohomolgy-Long exact sequence

So far the following maps are defined.

• Cochain map $\phi:H^k(A)\rightarrow H^k(B)$ induced cohomology map
  \begin{equation}
    \phi^{*}:H^k(A) \rightarrow H^k(B)
  \end{equation}
• For short exact sequence of cochain complexes \begin{equation}
    0  \rightarrow \mathcal{A} \xrightarrow{i} \mathcal{B} \xrightarrow{j} \mathcal{C} \rightarrow 0
  \end{equation}
  Connecting homomorphism map is
  \begin{equation}
    d^{*}:H^k(\mathcal{C}) \rightarrow H^{k+1}(\mathcal{A})
  \end{equation}
• Then the short exact sequence of cochain complexes
  \begin{equation}
    0  \rightarrow \mathcal{A} \xrightarrow{i} \mathcal{B} \xrightarrow{j} \mathcal{C} \rightarrow 0
  \end{equation}
  gives rise to long exact sequence in cohomology.
  \begin{equation}
   \cdots H^{k-1}(\mathcal{C}) \xrightarrow{d^{*}} H^k(\mathcal{A})  \xrightarrow{i^{*}} H^k(\mathcal{B}) \xrightarrow{j^{*}} H^k(\mathcal{C}) \xrightarrow{d^{*}} H^{k+1}(\mathcal{A}) \cdots
  \end{equation}
  
  

Cohomology-Connecting homomorphisms

A series of cochain complexes
\begin{equation}
  0 \rightarrow \mathcal{A} \rightarrow \mathcal{B} \rightarrow \mathcal{C} \rightarrow 0
\end{equation}
is ``short exact'' if $i,j$ are cochain maps and for each $k$
\begin{equation}
  0 \rightarrow A \xrightarrow{i} B \xrightarrow{j} C \rightarrow 0
\end{equation}
is short exact sequence of vector spaces.
Based on above sequence, we can define yet another new map called ``connecting homomorphism'' map

$d^{*}: H^k(\mathcal{C}) \rightarrow H^{k+1}(\mathcal{A})$

To analyze this connecting homomorphism,start with an element in $H^k(\mathcal{C})$ - say $c \in [c]$.
Since $C$ maps all elements to $0$ and because this is an exact sequence, image of $j$ will be onto. This means there exists an element $b\in B^k$ such that $c=j(b)$.
Because connecting homomorphism gives above commuting diagram, $C^{k+1}$ can be reached via $d(j(b))$ and also via $j(d(b))$. That is,
\begin{equation}
  d(j(b)) = j(d(b))
\end{equation}
However, $c=j(b)$. Then, $d(j(b))=d(c)=0$. Thus the element $db (\in B^{k+1}) \in ker\;j$.

In the $k+1$ diagram $ker\;j=im\;i$. That means there is an element $db = i(a)$ for some $a \in A^{k+1}$. Since $i$ is injective, element $a$ is unique. Injectiveness of $i$ also means $i(da)=d(ia)=db=0$ which shows $a$ is co-cycle and defines a conjugacy class $[a]$.

The defining equation for connecting homomorphism is

\begin{equation}
 d[c] = [a] \in H^{k+1}(A)
\end{equation}

Cohomology of Cochain complex

Recall that the cochain $\mathcal{C}$ complex is not an exact sequence (condition $im\;d_{k-1}=\ker\:d_k$ won't hold). The following holds

$im\;d_{k-1} \subset ker\;d_k$.

This gives us an opportunity to define quotient space

$H^k(\mathcal{C})$ as $ker\;d_k / im\;d_{k-1}$ which measures cochain complex fails to be exact at $k$.

Terminology:

$ker\;d$ is k-cocyle or closed forms(DeRahm cohomology) and $im\;d$ is k-coboundary or exact forms (DeRahm cohomology). Elements of $H^k(\mathcal{C})$ are equivalent classes $[c]$ for $c \in ker\;d_k$ is called cohomology class.

cochain map:

Between any two cochain complexes $\mathcal{A}, \mathcal{B}$ one can define a cochain map $\phi:\mathcal{A} \rightarrow \mathcal{B}$ - a collection of linear maps $\phi_k:A_k \rightarrow B_k$. If $d_1,d_2$ are corresponding differential operators for $\mathcal{A},\mathcal{B}$, drawing a commuting diagram shows

$d_2\circ \phi_k = \phi_{k+1} \circ d_1$

Nice thing about this map is that induces map $\phi^{*}:H^k(\mathcal{A}) \rightarrow H^k(\mathcal{B})$ between cohomologies. This map is well defined because it takes exact forms to exact forms and closed forms to closed forms.

For $a \in Z^k(\mathcal{A})$ ie closed forms of $\mathcal{A}$ at $k$, $d(\phi(a))=\phi(d(a))=0$ and for $b \in \mathcal{A}^{k-1}$, easy to see that $\phi(d(b))=d(\phi(b))$.

Vector spaces-First isomorphism theorem

Let $T:V \rightarrow W$ be a linear transformation between vector spaces $V$ and $W$.

Then, $\tau:T/ker(W) \rightarrow Im(W)$ induces an isomorphism given by $\tau(v+ker(T)) = T(v)$.

First we need to establish that if $v+ket(T)$ is replaced by $v'+ker(T)$ for $v,v'$ in the same coset ie $v-v' \in ker(T)$, then  $T(v)=T(v')$. That is, we need to establish that above map is well defined.

Notice,

$T(v) = T( (v'-v)+v' ) = T(v-v')+T(v') = T(v')$

Then we need to establish that the map $\tau$ is a linear map.

That is, for $v,v' \in V$, we need to show that $\tau(v+ker(T) + v'+ker(T))=\tau(v+ker(T))+\tau(v'+ker(T))$.

Indeed,  $\tau(v+ker(T) + v'+ker(T)) = T(v+v'+ker(T)) =T(v)+T(v')=\tau(v+ker(T))+\tau(v'+ker(T)$.

And

$\tau(\alpha (v+ker(T))) = \tau(\alpha v + \alpha  ker(T) ) = T(\alpha v) = \alpha T(v) = \alpha \tau(v+ker(T))$.

Thus the map T/ker(W)$ is a linear map.

To prove isomorphism, we need to show that this map is one-one and onto.

For one-one, if $\tau(v+ker(T))=0$, need to show that $v+ker(T)=0$ which is a direct result of the observation that if $\tau(v+ker(T))=T(v)=0$, then $v \in ker(T)$.

For onto, just note any element of $im(T)$ can be written as $T(v)$ for some $v \in V$ and thus equal to $\tau(v+im(T))$.

Theorem  (Universal mapping property for quotient spaces). Let $F$ be a field, $V,W$

vector spaces over $F$, $T : V → W$ a linear transformation, and $U \subset V$ a subspace.

If $U \subset ker(T)$, then there is a unique well-defined linear transformation

$\tau : V/U → W$ given by $\tau(v + U) = T(v)$.

 

Cohomology-exact sequences-1

A sequence of homomorphisms of vector spaces

$A \xrightarrow{f(x)} B \xrightarrow{g(x)} C$

is called "exact sequence" if $im f = ker g$.

One way of thinking about is as follows. Assume that $f(x)=g(x)=d$. Assume that $d$ applied to any element "dirties" it and second application $d$ to "dirtied" element sends it to $0$. Thus image of $d$ or $f$ is "dirtied" and because $g$  or second $d$ sends all such "dirtied" elements to zero, clearly $im\; d (or f)  = ker\; d( or g)$.

Short exact sequence has the form $0 \rightarrow A \rightarrow B \rightarrow C \rightarrow 0$.

Note for a sequence to be exact all the terms except for the first and last need to be exact.

The sequence $0 \xrightarrow{f} A \xrightarrow{g} B$ exact means $im\;f=ker;g=0$. Since only element in $ker\;g$ is $0$, $g$ is injective.

Similarly, in case $A \xrightarrow{f} B \xrightarrow{g} 0$, then all of $B$ is $ker\;g$. Hence, $im\;f=ker\;g=B$ and $f$ is surjective.

Problem 24.1 (Tu - An Introduction to Manifolds)

Given an exact sequence,
$A \xrightarrow{f(x)} B \xrightarrow{g(x)} C$

Show that $f$ is surjective iff $g$ is zero map.

Prf:

Assume $g$ is zero map. Then $ker\;g=B$. Using this in the definition of exact sequence results in $im\;f=ker\;g=B$. Hence $f$ is surjective.

Assume $f$ is surjective. From exact sequence definition, this means $im\;f=ker\;g=B$. $ker\;g=B$ implies $g$ is a zero map.

Show that $f$ is zero map iff $g$ is injective.

Prf:

Assume $g$ is injective. This means $ker\;g=0$. Using definition of exact sequence, results in $im\;f=ker\;g=0$. This $f$ is zero map.

Assume $f$ is zero map which means $im\;f=0$. Exact sequence implies $ker\;g=0$.Hence, $g$ is injective.

Problem 24.2. Four term exact sequence.

Four term sequence of vector spaces $0 \rightarrow A \xrightarrow{f} B \rightarrow 0$ is exact iff $f: A \rightarrow B$ is an isomorphism.

Prf:

Assume $f$ is an isomorphism which means $f$ is an injective and surjective function. $f$ is injective means $ker\;f=0$. And this is clearly image of previous zero map. $f$ is surjective and subsequent map is zero map. Then $im\;f$ is same as kernel of subsequent map.Both the conclusions yield an exact sequence.

Assume sequence is exact. Then image of zero map which is zero is clearly in kernel of $f$. Image of $f$ is same as kernel of subsequent (zero map). Hence $f$ is surjective. Thus $f$ is an isomorphism.

If $A \xrightarrow{f} B \rightarrow C \rightarrow 0$ is exact, then $C=coker\;f = \frac{B}{im\;f}$.

Rewrite sequence as

$A \xrightarrow{f} B \xrightarrow{g} C \rightarrow 0$

Given the sequence is exact, $im\;f=ker\;g$. Cokernel of $f$ is defined as $B/im\;f$. This can be written as $B/ker\;g$. First isomorphism theorem yields $B/ker\;g \cong im \;g$. However $im\;g = ker(C\rightarrow 0)$ which is all of $C$. Hence,
$B/ker\;g \cong C$.

Cohomology product structures and ring structure.

The product structure of wedge forms induces a product structure on Cohomoloy classes.

If $[\omega] \in H^{k}(M)$ and $[\tau] \in H^{k}(M)$ on a manifold $M$, then natural way to define the product structure is

$[\omega] \wedge [\tau] = [\omega \wedge \tau] \in H^{k+l}(M)$.

Know that $\omega,\tau$ are closed forms. So first we need to establish that the class $[\omega \wedge \tau]$ is a closed form. Note,

$d[\omega \wedge \tau] = d\omega \wedge \tau + (-)^k \omega \wedge d \tau = 0$.

Hence, $[\omega \wedge \tau]$ is a closed form.

Since, we are dealing with classes here, we need to show that if representative $\tau$ is replaced by exact form $\tilde{\tau}= \tau + d\eta$, then we need to show that

$d[\omega \wedge \tilde{\tau}] = d\omega \wedge \tau + (-1)^{k} \omega \wedge d\eta$

Thus, $\omega \wedge \tilde{\tau}$ is equal to $d[\omega \wedge \eta]$. Hence, closed.

• For a manifold $M$ of dimension $n$, the direct sum is $H^{*}(M) = \oplus_{k=1}^{n} H^{k}(M)$
• Thus $\omega \in H^{*}(M$, can be written as $\omega=\omega_0+\omega_1+\cdots+\omega_n$ where $\omega_{i} \in H^{i}(M)$.
• Product of differential forms defined on $H^{*}(M)$ gives $H^{*}(M)$ a ring structure - called "Cohomology ring".
• Since product of differential forms is anticommutative, the ring is anticommutative.
• Direct sum gives Cohomology ring a graded algebra structure.
• Thus, $H^{*}(M)$ is anticommutative graded ring.