\begin{equation}
0 \rightarrow \mathcal{A} \rightarrow \mathcal{B} \rightarrow \mathcal{C} \rightarrow 0
\end{equation}
is ``short exact'' if $i,j$ are cochain maps and for each $k$
\begin{equation}
0 \rightarrow A \xrightarrow{i} B \xrightarrow{j} C \rightarrow 0
\end{equation}
is short exact sequence of vector spaces.
Based on above sequence, we can define yet another new map called ``connecting homomorphism'' map
$d^{*}: H^k(\mathcal{C}) \rightarrow H^{k+1}(\mathcal{A})$
To analyze this connecting homomorphism,start with an element in $H^k(\mathcal{C})$ - say $c \in [c]$.
Since $C$ maps all elements to $0$ and because this is an exact sequence, image of $j$ will be onto. This means there exists an element $b\in B^k$ such that $c=j(b)$.
Because connecting homomorphism gives above commuting diagram, $C^{k+1}$ can be reached via $d(j(b))$ and also via $j(d(b))$. That is,
\begin{equation}
d(j(b)) = j(d(b))
\end{equation}
However, $c=j(b)$. Then, $d(j(b))=d(c)=0$. Thus the element $db (\in B^{k+1}) \in ker\;j$.
Since $C$ maps all elements to $0$ and because this is an exact sequence, image of $j$ will be onto. This means there exists an element $b\in B^k$ such that $c=j(b)$.
Because connecting homomorphism gives above commuting diagram, $C^{k+1}$ can be reached via $d(j(b))$ and also via $j(d(b))$. That is,
\begin{equation}
d(j(b)) = j(d(b))
\end{equation}
However, $c=j(b)$. Then, $d(j(b))=d(c)=0$. Thus the element $db (\in B^{k+1}) \in ker\;j$.
In the $k+1$ diagram $ker\;j=im\;i$. That means there is an element $db = i(a)$ for some $a \in A^{k+1}$. Since $i$ is injective, element $a$ is unique. Injectiveness of $i$ also means $i(da)=d(ia)=db=0$ which shows $a$ is co-cycle and defines a conjugacy class $[a]$.
The defining equation for connecting homomorphism is
\begin{equation}d[c] = [a] \in H^{k+1}(A)
\end{equation}
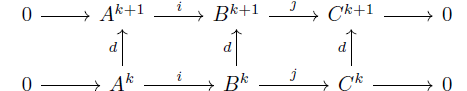

No comments:
Post a Comment