In
general, in order to classify somethings, we use an invariant. For
example if one is to classify a bunch of books, one can use broad
classification such as fiction vs non-fiction. And classification
possibilities are more depending on the diversity of the book
collection. In case of fiction vs non-fiction classification, the
invariant is if a book belongs to fiction or non-fiction. This is
nothing new. Similar concepts of classification is used in all fields of
sciences including social sciences.
While
classifying books - fiction vs non-fiction, we abstract out type of
book while removing all other information such as big book, small book,
physics book or bible.
In
Topology, in a similar fashion we ignore actual geometric shapes, areas
etc and focus on whether a space can be deformed continuously into a
smaller subset of spaces. When this deformation is taking place, certain
things remain invariant.
To
see this, assume you have a yet to be inflated balloon where you draw
letter "A". Clearly, the letter "A" has one closed loop. As you inflate
the balloon, the closed loop becomes larger and gets distorted - but
still very much visible. This means such closed loops are invariant
under continuous deformation.
Whereas
in Topology, the spaces are abstract, when you add extra structure to
these spaces as is done in smooth manifolds, the machinery of Linear
Algebra can be deployed to perform actual, tangible computations.
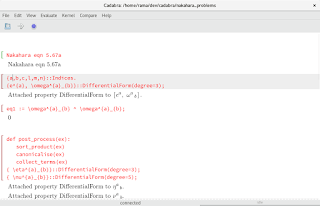
For
any $k$ form $\omega$, "closed" form means $d\omega=0$. "Exact" form
means $\omega=d\tau$ for a form $\tau$ which is a $k-1$ form.
One way to remember these definition is, $d\omega=0$ and since $0$ looks like a closed loop, one can remeber $d\omega=0$ as closed forms.
Let
$Z^k(M)$ on a smooth manifold $M$ be vector space of closed forms (think Z for zero) and
similarly, let $B^k(M)$ be vector space of exact forms.
Since $d^2\omega = 0$ for any form $\omega$, the exact forms are all closed as $d\omega=d(d(\tau)=d^2\tau=0$.
But not all closed forms are exact forms.
Since,
both $B^k(M),Z^k(M)$ are vector spaces, we can form a quotient space
$Z^k(M)/B^k(M)$ using the vector space equivalences.
The quotient $H^k(M)=Z^k(M)/B_k(M)$ is called de Rahm Cohomology. This is an invariant of Manifolds under certain conditions which will be noted later.
Since $H^k(M)$ is vector space quotient, for any differential forms $\omega,\omega'$, this means
$\omega' - \omega \in B^k(M)$ means $\omega' \tilde{} \omega$ in $Z^k(M)$.
This means the following relation is satisfied.
$\omega' = \omega + d\nu$.