Cohomology - motivating example

Concept of vector fields as gradients of functions is well established. However, sometimes taking curl of vectors also results in vector fields. These concepts lead to certain simplifications when computing line integrals.

The following illustrative example is from Tu's "Introduction to Manifolds".

Let $F(x,y)=(P(x,y),Q(x,y))$ be a vector field defined on an open set $U$ in $R^2$. Let $C$ represent a parameterized curve defined by $c(t)=(x(t),y(t))$ where $t \in [a,b]$ as it moves from point $A$ to $B$ on $U$. The total work done by a particle moving along this path is given by line integral $\int_C P(x,y)dx+Q(x,y)dy$.

If vector field is a gradient of a scalar function the line integral is easy to compute using Stoke's theorem.

$F=grad(f) = (f_x,f_y)$

where $f_x =\frac{\partial f}{\partial x}$ and
$f_y =\frac{\partial f}{\partial y}$

$\int_C f_x dx+f_y dy = \int_C df = f(B)-f(A)$.

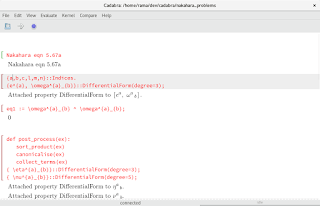
A necessary condition for $F$ to be grad of a scalar function $f$ is

$P_y = f_{xy}=f_{yx}=Q_x$.

The question is now the following:

If $Q_x-P_y=0$, is the vector field $F=(P,Q)$ gradient of some scalar function $f$ on $U$?

By correspondence between vector fields and 1-forms in $R^2$, we have,

$F=(P,Q) <-> \omega = Pdx + Qdy$

$grad f = (f_x,f_y) <->d\omega = f_x dx + f_y dy$

$Q_x-P_y=0 <-> d\omega = (Q_x-P_y)dx \wedge dy =0$.

So the question is, if $\omega =f _x dx+f_ydy$ is closed ie. $d\omega=0$ is it exact?

Answer is sometimes Yes and sometimes No and depends on $U$.

Cadabra Software

Cadabra software is Field theory motivated approach to Computer Algebra Systems (CAS for short). It can be downloaded from https://cadabra science/


There are some very nice tutorials and user notebooks in this site. I installed cadabra on opensuse linux (leap). I could only use their interface cadabra2-gtk. Had issues downloading other interfaces because of incompatibilities of boost library versions Leap is supporting.


cadabra2-gtk launches Cadabra notebook which behaves like Jupyter notebook. There is supposed to be command completion which didn't work for me.



Nice thing about Cadabra is its elegant latex support. Latex is built into commands directly. A sample session is shown below:

Cadabra SW: Applying to some exercises in Nakahara

Tests on differential forms:


Test 1: If $\omega$ is a differential form of odd dimension - say 3, then $\omega  \wedge \omega = 0 $. This is the attempt to let Cadbra solve this wedge form.


Nakahara eqn 5.67a

Cadabra code:

-----------------

{a,b,c,l,m,n}::Indices.

{e^{a}, \omega^{a}_{b}}::DifferentialForm(degree=3);

\(\displaystyle{}\text{Attached property DifferentialForm to }\left[e^{a}, \omega^{a}\,_{b}\right].\)

eq1 := \omega^{a}_{b} ^ \omega^{a}_{b};

0

Nice! Solves this. Test 2: Now we want to show explicitly - that is using numeric indices for $q,r$ the following expression:

$\eta \wedge \nu = (-1)^{qr} \nu \wedge \eta$.

Cadabra code:

-----------------

def post_process(ex):

sort_product(ex)

canonicalise(ex)

collect_terms(ex)

{ \eta^{a}_{b}}::DifferentialForm(degree=3);

{ \nu^{a}_{b}}::DifferentialForm(degree=5);

\(\displaystyle{}\text{Attached property DifferentialForm to }\eta^{a}\,_{b}.\)

\(\displaystyle{}\text{Attached property DifferentialForm to }\nu^{a}\,_{b}.\)

eq2 := \eta^{a}_{b} ^ \nu^{a}_{b}; eq3 := \nu^{a}_{b} ^ \eta^{a}_{b};

\(\displaystyle{}\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}\)

\eta^{a}_{b} ^ \nu^{a}_{b}

\(\displaystyle{}-\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}\)

-\eta^{a}_{b} ^ \nu^{a}_{b}

Cadabra code:

---------------

eq2 + eq3;

combine(_);

\(\displaystyle{}\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}-\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}\)
\eta^{a}_{b} ^ \nu^{a}_{b}-\eta^{a}_{b} ^ \nu^{a}_{b}

\(\displaystyle{}0\)

0





Exercise 5.15: Let $\xi \in \Omega^{q}(M)$ and $\omega \in \Omega^{r}(M)$.

Show that $d(\xi \wedge \omega) = d\xi \wedge \omega + (-1)^{qr} \xi \wedge d\omega$.

For simplicity, we shall set $q=3$ and $r=5$ - thus inducing a negative in the expression.
Using the following link is nice: https://cadabra.science/notebooks/exterior.html

Cadabra code:

-----------------

\xi::DifferentialForm(degree=3);

\omega::DifferentialForm(degree=5);

\(\displaystyle{}\text{Attached property DifferentialForm to }\xi.\)
\(\displaystyle{}\text{Attached property DifferentialForm to }\omega.\)


Add definition of exterior derivative.

Cadabra code:

-----------------

d{#}::ExteriorDerivative;

d{#}::LaTeXForm("{\rm d}").


\(\displaystyle{}\text{Attached property ExteriorDerivative to }d{\#}.\)
ext1 := d{ \xi ^ \omega };
\(\displaystyle{}{\rm d}\left(\xi\wedge \omega\right)\)

Cadabra code:

-----------------

d(\xi ^ \omega)
product_rule(_);


\(\displaystyle{}{\rm d}{\xi}\wedge \omega-\xi\wedge {\rm d}{\omega}\)
d(\xi) ^ \omega-\xi ^ d(\omega)


This demonstrates equation $5.69$ in Nakahra for even and odd indices.

Field Theory - Theorem 2

 

Algebraic:

There exists a polynomial $f$ with coefficients in field $K$ such that $f(u)=0$. In this case, we say $u$ is algebraic over $K$.

Transcendental:

There exists no polynoimal $f$ with coefficients in field $K$ such that $f(u)=0$ with the exception of zero polynomial. In this case, we say $u$ is trascendental over $K$.

A field $L$ containing field $K$ is considered algebraic over $K$ if every element of $L$ is algebraic over $K$.
 
Theorem 2:
 
Suppose $K$ is a field, $u$ an element of larger field, and suppose that $u$ is algebraic over $K$. Let $f$ be a monic polynomial with coefficients in $K$ of the minimal degree $n$ such that $f(u)=0$. Then
(a) $f$ is unique.
(b) $f$ is irreducible over $K$.
(c) $1,u,u^2,\cdots,u^{n-1}$ form a vector space basis for $K(u)$ over $K$.
(d) $[K[u]:K]=n$.
(e) A polynomial $g$ with coefficients in $K$ satisfies $g(u)=0$ iff $g$ is a multiple of $f$.

Proof:

Assume that there is another polynomial $f'$, and let $f_0=f-f'$. Since, both $f$ and $f'$ are monic, the leading terms gets eliminated and $f_0$ becomes a polynomial of degree less than $n$. This means, we have $f_0$ a polynomial with degree less than $n$ going to zero whenever $f,f'$ go to zero. However, this is a contradiction $f$ is supposed to be of minial degree.

$f$ is irreducible. Assume otherwise and write $f=hg$ where $h,g$ are polynomials of degree (obviously less than n). When $f$ goes to zero, one or both of $g,h$ will go to zero, thus contradicting the fact that $f$b is of minimal degree.

Linear relation between $1,u,u^2,\cdots,u^{k-1}$ indicates that there exists a polynomial $g(u)=0$ of degree less than $n$, thus proving that $1,u,u^2,\cdots,u^{n-1}$ form a linearly independent set for $K$.

All we need to show is that $T=K[u]$ is a field. Given all multiplicatons and additions we have been performing so far, not difficult to see that $T$ is a ring.

Next we need to show that $u^k \in T$. Clearly, $1,u,u^2,\cdots,n^{n-1} \in T$.
Now set an element $u^{k-1} = 1+u+u^2+\cdots+u^{n-1}$. Multiply both sidees by $u$. Then, $u^k = u+u^2+u^3+\cdots+u^n$. Since $u^n$ can be expressed in terms of $1,u,u^2,\cdots,u^{n-1}$, we have $u^k$ as a linear combination of these basis elements. Hence $u^k \in T$.

To show that $T$ is a field, we also need to show that every element has an inverse. Indeed if $g$ is another polynomial of degree less than $n$, given that $f$ is irreducible, we will have $gcd(f,g)=1$ which means there exists polynomials $r,s$ of degree less than $n$ such that $fr+gs = 1$. Clear that when $f$ gets sent to zero, the expression $gs=1$ indicating that $s$ is inverse of the $g$.

If $g$ is another polynomial with coefficients in $K$ such that $g(u)=0$ then $g$ is a multiple of $f$. If $g$ is not a multiple of $f$ (which is irreducible) then $gcd(f,g)=0$. This means that there are two polynomials $r,s$ such that $fr+gs=1$. Since $f(u)=0$, then $fr=0$ and $g(u)=0$ means $gs=0$ leading to contradiction. Hence, $g$ is a multiple of $f$.

Field extensions-Theorem 1

Notice the following tower of fields.

 Base field is $K=Q$, intermediate field is $L=Q(\sqrt{3})$ and top field is $M=Q(\sqrt{7})$.
Field $L=Q(\sqrt{3})=\{a+b\sqrt{3}|a,b \in Q\}$.
Field $M=Q(\sqrt{3})=\{a+b\sqrt{3}+c\sqrt{7}+d\sqrt{7x3=21}|a,b,c,d \in Q\}$. 

Note that the field $M$ is a vector space over $L$ and $K$. Indeed, from the expression $M=Q(\sqrt{3})=\{a+b\sqrt{3}+c\sqrt{7}+d\sqrt{7x3=21}|a,b,c,d \in Q\}$ one can see that $M$ as vector space over $K$ has dimension $4$.
That is $[M:K]=4$.
There is another way of expression $M$ as a vector space over $L$. 

Letting $u_1,u_2$ be elements of this form $u_1=a+b\sqrt{3}$ and $u_2=c+d\sqrt{3}$, one can express elements of $M$ as $u_1+\sqrt{7}(u_2)$.
That is $[M:L]=2$. Similarly $[L:K]=2$. Thus,
$[M:K]=[M:L][L:K]=2*2=4$.

First theorem of Field extensions formalizes these observations.

Theorem 1:Let $K,L,M$ be fields with $K\subset L \subset M$. Then $[M:K]$ is finite if and only if both $[M:L]$ and $[L:K]$  are finite and in that case $[M:K]=[M:L][L:K]$.
Proof is a generalization of above observations.
Assume that $[M:K]$ is finite, then consider $L$ as subspace of $M$ over $K$. As a subspace of finite vector space $[L:K]$ is finite. Any basis that spans $M$ over $K$ (for example, $\{a,b,c,d\}$ in above fields), also spans $M$ over $L$; hence, $[M:L]$ is also finite.

Assume the vector space $M$ over $L$ has $[M:L]=m$ and $L$ over $K$ has $[L:K]=n$, then we need to show that $[M:K]=mn$.

Let $z \in M$. $z$ can be expressed as $z=\sum_i u_i h_i$ where $h_i \in L$. And $h_i=\sum_j c_{ij}v_j$. Putting all this together, $z = \sum_i \sum_j c_{ij}u_i v_j$. $i,j$ range over $m$ and $n$. This is the spanning set for $M$ over $K$.

To show this is independent, we need to show that whenever $\sum_{ij} c_{ij} u_i v_j = 0$ we need to have $c_{ij}=0$.
$\sum_{ij} c_{ij} u_i v_j$ can be rewritten as $\sum_i h_i u_i$ where $h_i \in L$. Since $u_i$ form a basis for $M$ over $L$, we must have each $h_i=0$ and since this means $\sum c_{ij} v_j=0$ and independence of $v_j$ leads to each $c_{ij}=0$.

One consequence of this thoerem is that if the order of $M/L$ is a prime, then this precludes any fields between $M$ and $L$.

More examples of Galois groups

Let $F=Q$. Now, this time consider the polynomial $(x^2-2)(x^2-3)$. Clearly the roots of the polynomial are $\pm\sqrt{2},\pm\sqrt{3}$. The splitting field for this polynomials is $E(\sqrt{2},\sqrt{3}) = \{a+b\sqrt{2}+c\sqrt{3}+d\sqrt{6}|a,b,c,d, \in Q\}$. Notice, that $x^2=\sqrt{6}$ is also a root.

Dimension of $E$ is $4$ and easy to see that $E$ is a vector space over $F$.

To derive Galois group, we start listing out the automorphisms of the extended field $E$ that fix $F$.

Thus we are seeking $\sigma$ that takes a root of $x^2-2$ to a root of $x^2-2$. That is $\sigma(\sqrt{2})=\pm\sqrt{2}$. Similarly $\sigma(\sqrt{3}) = \pm \sqrt{3}$

The value of both these roots can be taken independently. The following lists all the automorphisms of that fix $F$.

Thus $G=Gal(E/F)=\{\sigma_1=Id,\sigma_2,\sigma_3,\sigma_4\}$

It is interesting to note that we have intermediate fields between $F$ and $E$. Naming them as $B_1=F$ and $B_5=E$, we have other fields $B_2=Q(\sqrt{2}),B_3=Q(\sqrt{3}),B_4=Q(\sqrt{6})$.

These nested fields are shown below:

 As vector spaces $Q(\sqrt{2})$ has dimension $2$. Same is true of other intermediate field $Q(\sqrt{3})$.Field $Q(\sqrt{2},\sqrt{3})$ has dimension $4$ over $E=Q$ has dimensions $2$ over $Q(\sqrt{2})$ and $Q(\sqrt{3})$.

These examples lay foundation for understanding theorems about field extensions.

Simple example of a Galois Group:

Let $Q$ be a field of rationals. Let $x^2-2$ be a polynomial with rational coefficients. That is, let $x^2-2 \in Q[x]$.

Since $\sqrt{2}$ is not a rational, the roots of equation $x^2-2$ will not be in $Q$. However, if we extend this field by adjoining $\sqrt{2}$, then we have a new field over which the polynomial $x^2-2$ has roots. This new field $Q(\sqrt{2})$ is called splitting field of the polynomial. Elements of this field have form $\{a+b\sqrt{2}|a,b \in Q\}$.

Let $K=Q,L=Q(\sqrt{2})$. 

We ask for all automorphisms of $L$  that fix $K$, namely $\phi:L \rightarrow L$ that fix $K$. These automorphisms must take a root of above polynomial to a root. Thus, we have two automorphisms.

$Q(\sqrt{2})$ should map to $\sqrt{2}$. Identity automorphism $Id$ meets this criteria. 

Consider automorphism $\phi_1(\sqrt{2})\rightarrow -\sqrt{2}$. Clearly, this will carry elements of $Q(a+b\sqrt{2}) \rightarrow a - b \sqrt{2}$. 

If we collect all these automorphisms into a set, we have a set consisting of $\{Id,\phi_1\}$

Clearly $\phi_1\circ\phi_1 = Id$. Hence, above set forms  a group of order $2$.  This Automorphism group is called Galois group denoted as $Gal(L/K)$.