Tests on differential forms:
Test 1: If $\omega$ is a differential form of odd dimension - say 3, then $\omega \wedge \omega = 0 $. This is the attempt to let Cadbra solve this wedge form.
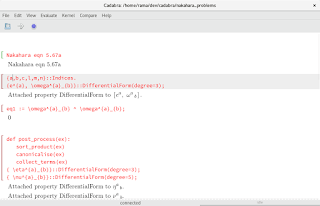
Nakahara eqn 5.67a
Cadabra code:
-----------------
{a,b,c,l,m,n}::Indices.
{e^{a}, \omega^{a}_{b}}::DifferentialForm(degree=3);
\(\displaystyle{}\text{Attached property DifferentialForm to }\left[e^{a}, \omega^{a}\,_{b}\right].\)
eq1 := \omega^{a}_{b} ^ \omega^{a}_{b};
0
Nice! Solves this. Test 2: Now we want to show explicitly - that is using numeric indices for $q,r$ the following expression:
$\eta \wedge \nu = (-1)^{qr} \nu \wedge \eta$.
Cadabra code:
-----------------
def post_process(ex):
sort_product(ex)
canonicalise(ex)
collect_terms(ex)
{ \eta^{a}_{b}}::DifferentialForm(degree=3);
{ \nu^{a}_{b}}::DifferentialForm(degree=5);
\(\displaystyle{}\text{Attached property DifferentialForm to }\eta^{a}\,_{b}.\)
\(\displaystyle{}\text{Attached property DifferentialForm to }\nu^{a}\,_{b}.\)
eq2 := \eta^{a}_{b} ^ \nu^{a}_{b}; eq3 := \nu^{a}_{b} ^ \eta^{a}_{b};
\(\displaystyle{}\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}\)
\eta^{a}_{b} ^ \nu^{a}_{b}
\(\displaystyle{}-\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}\)
-\eta^{a}_{b} ^ \nu^{a}_{b}
Cadabra code:
---------------
eq2 + eq3;
combine(_);
\(\displaystyle{}\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}-\eta^{a}\,_{b}\wedge \nu^{a}\,_{b}\)
\eta^{a}_{b} ^ \nu^{a}_{b}-\eta^{a}_{b} ^ \nu^{a}_{b}
\(\displaystyle{}0\)
0
Exercise 5.15: Let $\xi \in \Omega^{q}(M)$ and $\omega \in \Omega^{r}(M)$.
Show that $d(\xi \wedge \omega) = d\xi \wedge \omega + (-1)^{qr} \xi \wedge d\omega$.
For simplicity, we shall set $q=3$ and $r=5$ - thus inducing a negative in the expression.
Using the following link is nice: https://cadabra.science/notebooks/exterior.html
Cadabra code:
-----------------
\xi::DifferentialForm(degree=3);
\omega::DifferentialForm(degree=5);
\(\displaystyle{}\text{Attached property DifferentialForm to }\xi.\)
\(\displaystyle{}\text{Attached property DifferentialForm to }\omega.\)
Add definition of exterior derivative.
Cadabra code:
-----------------
d{#}::ExteriorDerivative;
d{#}::LaTeXForm("{\rm d}").
\(\displaystyle{}\text{Attached property ExteriorDerivative to }d{\#}.\)
ext1 := d{ \xi ^ \omega };
\(\displaystyle{}{\rm d}\left(\xi\wedge \omega\right)\)
Cadabra code:
-----------------
d(\xi ^ \omega)
product_rule(_);
\(\displaystyle{}{\rm d}{\xi}\wedge \omega-\xi\wedge {\rm d}{\omega}\)
d(\xi) ^ \omega-\xi ^ d(\omega)
This demonstrates equation $5.69$ in Nakahra for even and odd indices.